Andreotti–Frankel theorem
In mathematics, the Andreotti–Frankel theorem from 1959 states that if  is a smooth affine variety of complex dimension
is a smooth affine variety of complex dimension  or, more generally, if
or, more generally, if  is any Stein manifold of dimension
is any Stein manifold of dimension  , then in fact
, then in fact  is homotopy equivalent to a CW complex of real dimension at most n. In other words
is homotopy equivalent to a CW complex of real dimension at most n. In other words  has only half as much topology.
has only half as much topology.
Consequently, if 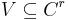 is a closed connected complex submanifold of complex dimension
is a closed connected complex submanifold of complex dimension  . Then
. Then  has the homotopy type of a
has the homotopy type of a 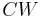 complex of real dimension
complex of real dimension 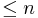 . Therefore
. Therefore
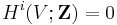 , for
, for 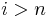
and
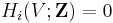 , for
, for 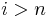 .
.
This theorem applies in particular to any smooth affine variety of dimension  .
.
References
- John Willard Milnor (1963), Morse Theory, Ch. 7.